机器学习算法常常需要大量的数学计算，尤其是一些需要迭代求解的算法。
优化算法和解线性方程时，当这些函数涉及到实数操作时，就要在数值精度和内存两者之间做权衡了。

4.1 上溢出和下溢出（Overflow and Underflow）

使用数字计算机表示连续变量时，需要用有限的bit来表示无限的实数。这意味着，对于大部分的实数，有精度上的损失。这样的误差叫做舍入误差。舍入误差包括Underflow和Overflow。

Underflow:当数值接近0时，被舍入为0。
Overflow:当数值逼近正负无穷时，数值变为Not-A-Number（NAN）。

Softmax函数就一个要同时处理Unverflow和Overflow的函数
$$ \text {softmax }(x)_i=\frac{\exp(x_i)}{\sum_{j=1}^{n}\exp (x_j)} $$
假设$x_i$为常数$c$，这时函数应该为$\frac{1}{n}$。当$c$为负且很大时，这时会出现Underflow；当$c$为正且很大时，竟会出现Overflow。用线性代数处理一下$z=x-\max(x_i)$，再求$\text {softmax}(z)$即可。

还有一个小的问题。分子的underflow可能会导致整个表达式为零。即，如果首先计算softmax函数，然后把结果传递给log函数，可能会得到$-\infty$。可以使用同样方法避免这个问题。

在使用算法时，可能不会考虑溢出问题，因为一些底层库的作者常常已经处理好这个问题了。当时，要时刻意识到这个问题。

4.2 Poor Conditioning

Condition是指函数输入变化时，它的输出变化的快慢。输入微小变化就能引起输出很大波动的的函数，对于科学计算来说，有问题。因为数据可能存在噪声（或预处理存在噪声），噪声很大程度影响了输出。

例如函数$f(x)=A^{-1}x$，其中$A \in R^{n \times n}$，且有特征值，那么它的condition number 就是
$$ \max_{i,j}\frac{\lambda_i}{\lambda_j} $$
这个比值就是幅度最大的特征值和幅度最小的特征值的比值。如果比值很大，那么矩阵的逆对输入就很敏感。

这种敏感是矩阵本身的特性，而不是求逆过程中的误差。这样的矩阵会放大预处理的误差。

4.3梯度下降最优化

大多数机器学习都会涉及到最优化；最优化是指最大化$f(x)$或最小化$-f(x)$。要最大化或最小化的函数叫做目标函数或准则；如果最小化它时，常常叫做代价函数、损失函数或误差函数。

最下滑函数，常常使用梯度下降法。但是在梯度为零的点，梯度没有为我们提供信息。梯度为零$f^{‘}(x)$的点，是关键点或驻点（critical points or stationary point）。梯度为零的点，可以是局部最小值，或者是局部最大值，也可能是鞍点(saddle point)。如下图：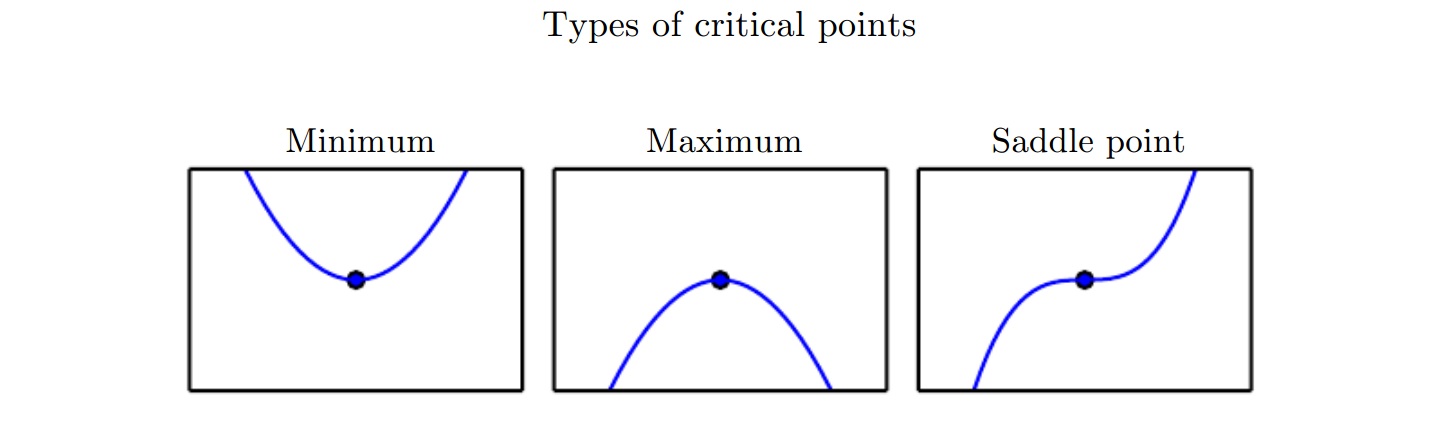

局部最小值可能不是全局最小值，全局最小才是最优。在深度学习中，优化的函数有许多局部最小值和鞍点；尤其是当优化目标函数为多维函数时。下图是一维情况的简单描述：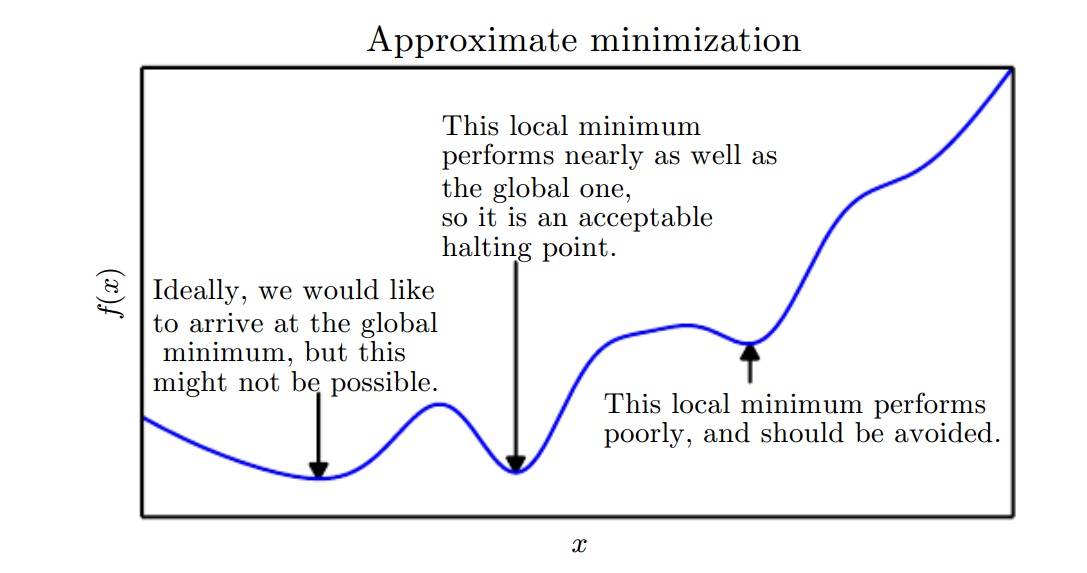

我们优化的函数，输入可能是多维的，但输入是一维的：$f:R^n \to R$。输入是多维时，对某一维变量求导就是偏导了$\frac{\partial}{\partial x_i}f(x)$。对函数就到得到的梯度就是一个向量了$\nabla_x f(x)$，其中每一个元素都是偏导。

在某个方向$u$（向量）上的导数为$\frac{\partial}{\partial \alpha} f(x + \alpha u) =u^T \nabla_x f(x)$。

最小化$f$就是找到一个方向，在这个方向上下降最快。实际上，梯度是上升最快的方向，其反方向就是下降最快的方向。沿着梯度反方向下降的方法，叫做最速下降法（steepest descent）或梯度下降（gradient descent）。

最速下降法使用如下：
$$ x^{'} = x - \epsilon \nabla_x f(x) $$
这里$\epsilon$叫做学习率，它指示在下降过程中的步长，可以设置不同的值。最流行的做法是把它设置为常数。有时，还用通过设置步长，防止梯度消失。还有一种设置步长的方法，通过计算不同$\epsilon$时，目标函数$f(x - \epsilon \nabla_x f(x))$的大小，来选择最优的学习率；这种策略叫做线性搜索。

梯度下降只能用在连续空间。但是其思想：通过一步步移动，找到最优点，可以用到离散空间。

4.3.1 Beyond the Gradient:雅克比矩阵和海森矩阵

对于输入和输出都是多维情况，这时求其偏导，可以得到雅克比矩阵（Jacobian Matrices）。函数$f:R^m \to R^n$，那么雅克比矩阵$J \in R^{n \times m}$，矩阵中的每个变量
$$ J_{i,j} = \frac{\partial}{\partial x_j}f(x)_i $$
对于函数$f:R^n \to R$，求它导数的导数，即二阶导数，可以得到海森矩阵。二阶导数告诉我们一阶导数随输入变量变化而变化的情况。二阶导数很重要，它可以告诉我们基于一阶导数梯度步长，将会引起多大提高。可以把二阶导数想象为衡量弯曲。例如，有一个二次函数，如果它二阶导数为零，那么它是一条直线，没有弯曲。假设梯度为1,如果二阶导数为负，那么其开口向下，函数$f(x)$下降幅度大于$\epsilon$；如果二阶导数为正，那么其下降小于步长。如下图：

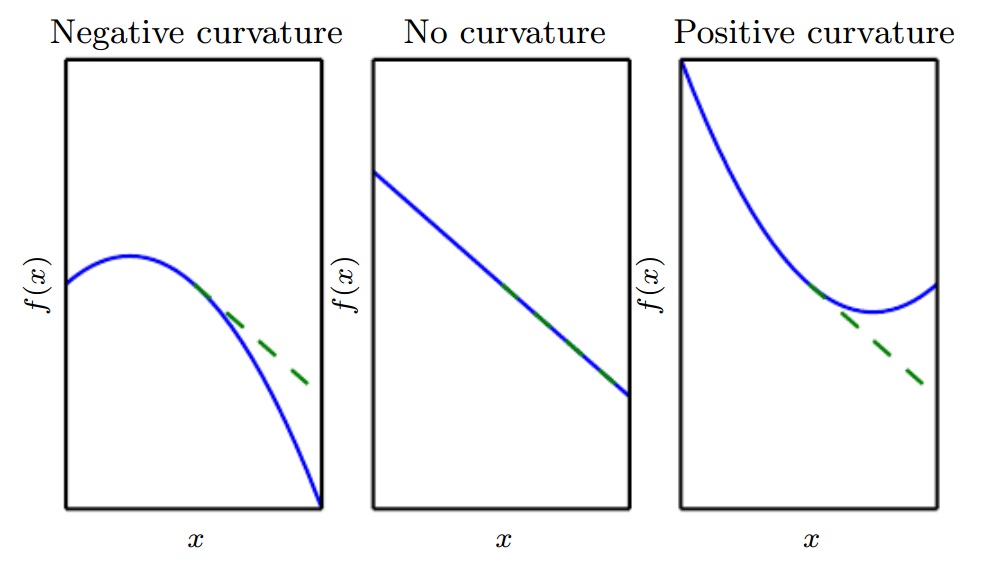
二阶导数定义的矩阵，叫做海森矩阵：
$$ H(f)(f)_{i,j}=\frac{\partial^2}{\partial x_i \partial x_j}f(x) $$
求导符合交换律，即：
$$ H(f)(f)_{i,j}=\frac{\partial^2}{\partial x_j \partial x_i}f(x) $$
即海森矩阵是对称矩阵$H{i,j} = H{j,i}$。海森矩阵是对称的实数矩阵，可以分解为特征值和特征向量，且特征值为实数。二阶微分，在某一方向$d$表示为$d^THd$，其中$d$是$H$的单位特征向量，在此方向上的值为特征向量对应的特征值。对于其他的方向，是单位特征向量的加权和。最大的特征值对应最大二阶导数，最小特征值对应最小二阶导数。

二阶导数的方向可以告诉我们梯度下降算法下降的幅度。用二阶泰勒级数在$x^{(0)}$处展开目标函数可以得到:
$$ f(x) \approx f(x^{(0)}) + (x - x^{(0)})^Tg+\frac{1}{2}(x-x^{(0)})^T H(x-x^{(0)})（x-x^{(0)}） $$
这里$g$是梯度，$H$是海森矩阵。如果学习率为$\epsilon$是学习率用$x^{(0)} - \epsilon g$代替$x$，可以得到：
$$ f(x^{(0)} - \epsilon g) \approx f(x^{(0)}) - \epsilon g^Tg + \frac{1}{2}\epsilon^2 g^THg $$
使用梯度下降算法，步长为 $\epsilon$时，下降大小为$- \epsilon g^Tg + \frac{1}{2}\epsilon^2 g^THg$。当后面一项比较大时，目标函数可能没有变小；当$g^THg$为负数或为零时，学习率为任何值，都会下降。在使用泰勒级数时，如果$\epsilon$比较大时，二项展开精度可能就不高。如果$g^THg$为正数，那么最佳学习率为
$$ \epsilon^* = \frac{g^Tg}{g^THg} $$
最坏情况下，当$g$和$H$的最大特征值对应的特征向量平行时，最佳步长为$\frac{1}{\lambda_{max}}$

二阶导数可以判断关键是是局部最小、局部最大、鞍点。关键点处$f^{‘}(x)=0$；如果$f^{‘’}(x)> 0$，意味着如果$f^{‘}(x)$向右移动大于零，向左移动小于零，即$f^{‘}(x-\epsilon)<0, f^{‘}(x+\epsilon)>0$f^{‘}(x-\epsilon)<0f^{‘}(x-\epsilon)<0f^{‘}(x-\epsilon)<0,可以得到此处为局部最小值。同理当$f^{‘}(x) = 0, f^{‘’}(x) < 0$时，此处为局部最大值。当$f^{‘}(x) = 0, f^{‘’}(x) = 0$，这时不能得到确切的结论，此时$x$可能为鞍点，或一段平坦区域。

对于多维情况，同一点不同方向导数不同。海森矩阵的condition number衡量二阶导数变化情况，如果海森矩阵的condition number是poor的，那么梯度下降性能不好。因为在某一点的一个方向，梯度可能下降很快，但是在另一个方向，梯度下降很慢；这时很难选择一个全局的学习率。如下图所示：

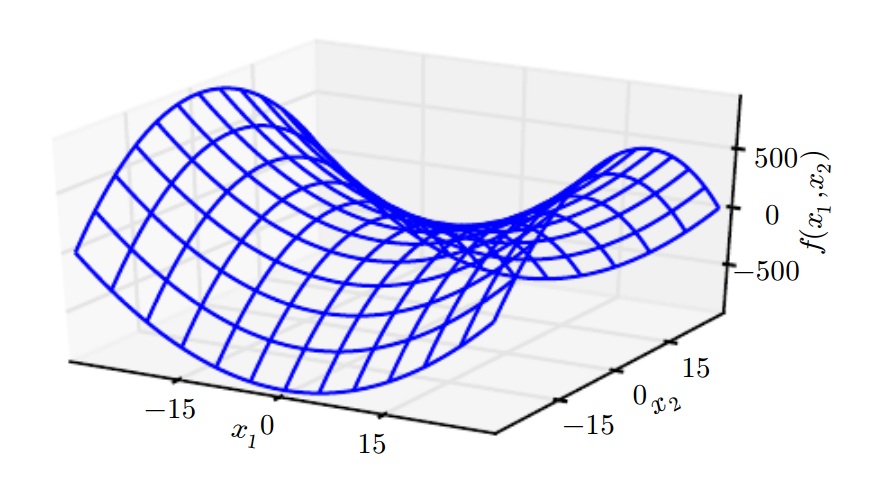
在上图中，方向[1,1]上的弯曲率最大，方向[1,-1]上的弯曲率最小。红色的线是梯度下降时，行走的路线。可以看到，来回走动，浪费很多步。

可以使用从海森矩阵中得到的信息来指导搜索。最简单的方法是牛顿法。牛顿法是基于二阶导数的泰勒展开的：
$$ f(x) \approx f(x^{(0)}) + (x - x^{(0)})^Tg+\frac{1}{2}(x-x^{(0)})^T H(x-x^{(0)})（x-x^{(0)}） $$
对于关键点，求解函数，得到
$$ x^* = x^{(0)} - H(f)(x^{(0)})^{-1} \nabla_x f(x^{(0)}) $$
当函数$f$是二次时，只需要一步即可跳到最优解。当函数不是正定的，但是可以近似为二次正定的，可以迭代使用上面公式，这样比梯度下降法要快。这在局部最小值附近时是个有用的特性，但是牛顿法只能在局部最小值附近来近似。

梯度下降是一阶导数的优化算法，牛顿法是二阶导数的最优化算法。这些最优化算法可以用到大多数的深度学习应用中，但是不确保一定有效。因为深度学习中，用到的函数十分复杂。有时需要给函数加上Lipschitz连续限制。Lipschitz连续函数为：
$$ \forall x, \forall y, |f(x) - f(y)| \leq \varsigma ||x-y||_2 $$
其中$\varsigma$是Lipschitz限制。这时一个很有用的特性，因为输入上的微小变量，将会引起输出上的微小变化。Lipschitz限制是一个弱限制，深度学习中的许多问题可以经过微小修改获取Lipschitz连续性。

在优化领域，最成功的领域是凸优化。凸优化通过许多强限制来加以保证。凸优化只能用来解决凸函数，海森矩阵为半正定的函数才是凸函数；这样的函数没有鞍点，局部最小值即为全局最小值。但是深度学习中，目标函数往往不是凸函数。凸函数优化只能用作深度学习的一个分支。

4.4 受限的优化问题

有时我们要在限制输入满足$x$一定条件情况来，来最小化目标函数。这就是受限的优化问题。

常常用的一种方法是把受限条件考虑到目标函数中，然后再来优化新的目标函数。

一种复杂的方法，是把受限问题转换为不受限的问题来解决。

Karush-Kuhn-Tucker(KKT)方法提供了解决受限问题的一种通用方法。这里介绍一种新的方法，拉格朗日乘子法或拉格朗日函数。

在定义拉格朗日函数前，先定义受限集合的描述，假设受限约束有m个等式和n个不等式描述。受限集合$S={x|\forall i,g^{(i)}=0 \quad \text{and} \forall j, h^{(j)} \leq 0}$。为每个约束引入新的变量$\lambda_i, \alpha_j$，它们叫做KKT乘子，拉格朗日函数定义如下：
$$ L(x, \lambda, \alpha) = f(x) + \sum_i \lambda_i g^{(i)}(x) + \sum_j \alpha_j h^{(j)}(x) $$
这样就可以用不受限的优化问题解决受限的优化问题。注意到只有存在可行点，那么$f(x)$就不能有无穷大值点，那么
$$ \min_{x} \max_{\lambda} \max_{\alpha, \alpha \geq 0} L(x, \lambda, \alpha) $$
和
$$ \min_{x \in S}f(x) $$
有相同的优化目标和结果集。这时因为满足
$$ \max_{\lambda} \max_{\alpha, \alpha \geq 0} L(x, \lambda, \alpha) = f(x) $$
违反
$$ \max_{\lambda} \max_{\alpha, \alpha \geq 0} L(x, \lambda, \alpha) = \infty $$
这条性质确保在可行性点不变情况下，非可行性点不会得到优化。

不等式的约束很有趣。如果$h^{(i)}(x^*)=0$，那么这个不等式就是激活的。否则，这个不等式就是没有激活的。如果一个约束没有激活，那么使用这个约束得到的解，至少是不使用这个约束时，问题的局部解。没有激活的约束也会排除一些解。例如一个凸优化问题，没有约束时，它的解的范围是全局任何点；也可以使用一些约束把它解的范围约束到一个集合范围内。但是在收敛处的点，不管约束有没有激活，它都是个stationary point。因为没有激活的约束$h^{(i)}$是负值，那么对于变形后的目标函数$\min{x} \max{\lambda} \max_{\alpha, \alpha \geq 0} L(x, \lambda, \alpha)$，将会有$\alpha_i=0$，因此可以得到$\alpha h(x)=0$，即约束$\alpha_i \geq 0$和$h^{(i)}(x) \leq 0$中，至少有一个是激活的。

泛化后的拉格朗日梯度为零，对于$x$约束和KKT乘数都必须满足，且$\alpha \odot h(x)=0$，这些约束叫做KKT条件。

4.5例子：线性最小平方

要最小化下面目标函数
$$ f(x) = \frac{1}{2}||Ax-b||_2^2 $$
第一步，求得梯度
$$ \nabla_x f(x) = A^T(Ax-b)=A^TAx-A^Tb $$
使用梯度下降，按照以下步骤

1、设置步长和容忍方差$\delta$
$\text {while} \quad ||A^TAx-A^Tb||_2 > \delta \quad do$
$\quad x \leftarrow x - \epsilon (A^TAx-A^Tb)$
$\text{end while}$

也可以使用牛顿法求解，因为函数是二次的，可以一步得到全局最优解。

如果给输入加上约束$x^Tx \leq 1$，得到拉格朗日函数
$$ L(x,\lambda) = f(x) + \lambda(x^Tx-1) $$
有约束问题变为无约束问题
$$ \min_x \max_{\lambda, \lambda \geq 0} L(x,\lambda) $$
朗格朗日函数对$x$求导，得到
$$ A^TAx - A^Tb + 2 \lambda x = 0 $$
得到的解的形式为：
$$ x = (A^TA+2\lambda I)^{-1}A^T b $$
$\lambda$幅度必须满足约束。对它求导
$$ \frac{\partial}{\partial \lambda}L(x,\lambda)=x^T x -1 $$
当$x$范数大于1时，上面导数为正；增大$\lambda$拉格朗日函数值随之增大。因为$x^Tx$的系数增大，所以$x^Tx$将会变小（因为我们在最小化朗格朗日函数）。如此重复，直到$\lambda$导数为零。